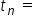Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
Above are the values for the first term and common difference for...
When a = 30, and d = 100
...
Above are the values for first term and common difference for an...
Above are the values for first term and common difference for an...
Above are the values for first term and common difference for an...
Above are the values for first term and common difference for an...
Above are the values for first term and common difference for an...
Above are the values for first term and common difference for an...
Above are the values for first term and common difference for an...
Above are the values for the first term and common difference for...
Above are the values for first term and common difference for an...
When a = 15 , and d = -4
...
Above are the values for first term and common difference for an...
When a = 1, and d = 4
...
Above are the values for first term and common difference for an...
When a = 25, and d = 6
...
When a = 38, and d = 10
...
When a = 6, and d = 10
...
When a = 7, and d = 10
...
When a = 23, and d = -100
...
When a = 8, and d = -100
...
When a = 18, and d = -9
...
When a = 11, and d = -3
...
When a = 35, and d = -5
...
When a = -9, and d = -2
...
When a = -2, and d = -8
...
When a = -38, and d = 200
...
When a = -24, and d = -5
...
When a = -36, and d = -10
...
When a = -19, and d = -20
...
When a = -26, and d = -6
...
When a = -14, and d = 9
...
When a = -7, and d = 7
...
When a = -31, and d = 9
...
When a = -11, and d = 200
...
When a = -4, and d = 7
...
When a = -29, and d = 5
...
When a = -21, and d = 2
...
When a = -14, and d = 9
...
When a = -36, and d = 20
...
When a = -16, and d = 20
...
When a = -26, and d = 20
...
When a = 3, and d = 200
...
When a = 31, and d = 200
...
When a = 26, and d = 5
...
Above are the values for first term and common difference for an...
When a = 30, and d = 100
...
When a = -33, and d = 10The rule for the Arithmetic...
When a = 16, and d = 18
...
When a = 28, and d = 30
...