Binomial Theorem Quiz
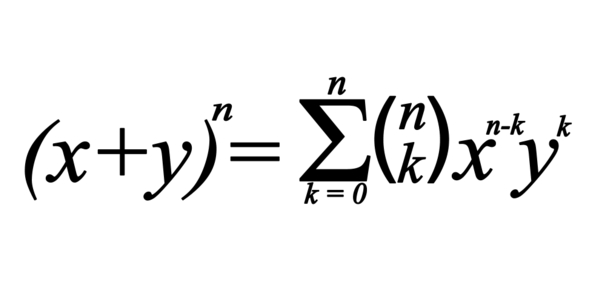
The Binomial Theorem is a quick way of expanding a binomial expression that has been raised to some power. Most students have issues when it comes to working out these problems, having some practice helps. Take up the Binomial theorem quiz below to sharpen your math skills. All the best!
Questions and Answers
- 1.
The binomial expansion of (1-b)^ is the same as that of (1+b)^n except that the coefficients have alternate + and - signs.
- A.
True
- B.
False
Correct Answer
A. TrueExplanation
The statement is true because when expanding the binomial (1-b)^n, the coefficients will have alternating positive and negative signs. This is because the binomial theorem states that the coefficients are given by the combination formula, which alternates between positive and negative values. Therefore, the binomial expansion of (1-b)^n will have the same coefficients as the expansion of (1+b)^n, but with alternating signs.Rate this question:
-
- 2.
In the expansion of (x^3-2/x^2)^10, find the coefficient of 1/x^5.
- A.
13440
- B.
3360
- C.
-15360
Correct Answer
C. -15360Explanation
To find the coefficient of 1/x^5 in the expansion of (x^3-2/x^2)^10, we need to find the term that contains 1/x^5. This term can be obtained by choosing the x^3 term from the first factor (x^3)^10 and the (-2/x^2) term from the second factor (-2/x^2)^10. The exponent of x^3 is 10, and the exponent of (-2/x^2) is also 10. Multiplying these exponents gives us x^30 * (-2)^10 / x^20 = -2^10 * x^10 / x^20 = -1024 * x^10 / x^20 = -1024 / x^10. The coefficient of 1/x^5 is therefore -1024. However, since the question asks for the coefficient of 1/x^5, we need to multiply -1024 by x^5, resulting in -1024x^5. Therefore, the correct answer is -1024.Rate this question:
-
- 3.
There is no difference between the power n and the expansion of the binomial theorem.
- A.
True
- B.
False
Correct Answer
B. FalseExplanation
The given statement is false. There is a difference between the power n and the expansion of the binomial theorem. The binomial theorem is a formula used to expand expressions of the form (a + b)^n, where a and b are numbers and n is a positive integer. The expansion involves a series of terms with coefficients and powers of a and b. On the other hand, the power n refers to the exponent in an expression, which can be any number, not necessarily a positive integer. Therefore, the statement is incorrect.Rate this question:
-
- 4.
Find the term x^3 in the expansion of (1+5)^2(1-2x)^6. 150x^3
- A.
150x^3
- B.
140x^3
- C.
91x^3
Correct Answer
B. 140x^3Explanation
To find the term x^3 in the expansion of (1+5)^2(1-2x)^6, we need to use the binomial theorem. The binomial theorem states that the term with x^k in the expansion of (a+b)^n is given by the formula: (n choose k) * a^(n-k) * b^k. In this case, we have (1+5)^2(1-2x)^6, so a = 1+5 = 6, b = 1-2x, and n = 6. Plugging these values into the formula, we get: (6 choose 3) * 6^(6-3) * (1-2x)^3 = 20 * 216 * (1-2x)^3 = 4320 * (1-2x)^3. Therefore, the term x^3 is 4320 * (1-2x)^3, which is equal to 140x^3 after simplifying.Rate this question:
-
- 5.
In the expansion of (2+3x)^n, the coefficients of x^3 and x^4 are in the ratio of 8:15. Find the value of n.
- A.
10
- B.
8
- C.
3
Correct Answer
B. 8Explanation
The ratio of the coefficients of x^3 and x^4 in the expansion of (2+3x)^n is 8:15. This means that the coefficient of x^3 is 8 times smaller than the coefficient of x^4. In the expansion of (2+3x)^n, the coefficient of x^3 is given by the formula (n choose 3) * 2^(n-3) * (3^3), where (n choose 3) represents the binomial coefficient. Similarly, the coefficient of x^4 is given by (n choose 4) * 2^(n-4) * (3^4). By comparing these two expressions, we can set up the equation (n choose 3) * 2^(n-3) * (3^3) = 8 * (n choose 4) * 2^(n-4) * (3^4). Simplifying this equation, we can find the value of n, which is 8.Rate this question:
-
- 6.
Who created the special triangle?
Correct Answer
Blaise PascalExplanation
Blaise Pascal is credited with creating the special triangle, also known as Pascal's triangle. This triangular arrangement of numbers has various mathematical properties and is used in fields such as combinatorics, probability theory, and algebra. It is named after Pascal because he was the first to describe its properties and applications in his work "Traité du triangle arithmétique" published in 1665. Pascal's triangle is formed by starting with a row of 1's and each subsequent row is created by adding the adjacent numbers in the row above.Rate this question:
- 7.
Find the 7th term of (2+x)^10.
- A.
3360x^6
- B.
3000x^6
- C.
4500x^7
Correct Answer
A. 3360x^6Explanation
The 7th term of (2+x)^10 can be found using the binomial theorem. The general formula for finding the kth term of (a+b)^n is given by (n choose k) * a^(n-k) * b^k. In this case, a = 2, b = x, and n = 10. Plugging in these values and simplifying the expression, we get (10 choose 6) * 2^4 * x^6 = 210 * 16 * x^6 = 3360x^6. Therefore, the 7th term of (2+x)^10 is 3360x^6.Rate this question:
-
- 8.
BINOMIAL , in mathematics, a word first introduced by Robert Recorde (1557) to denote a quantity composed of the sum or difference to two terms; as a+b, a-b.
- A.
True
- B.
False
Correct Answer
A. TrueExplanation
The explanation for the given correct answer is not available.Rate this question:
-
- 9.
Find the coefficient of x^6 in (1-3x)^8
- A.
20412
- B.
10512
- C.
23110
Correct Answer
A. 20412Explanation
To find the coefficient of x^6 in (1-3x)^8, we can use the binomial theorem. The binomial theorem states that the coefficient of x^k in the expansion of (a+b)^n is given by the binomial coefficient C(n,k) multiplied by a^(n-k) multiplied by b^k.
In this case, a=1, b=-3x, n=8, and k=6. Plugging these values into the formula, we get C(8,6) * 1^(8-6) * (-3x)^6 = C(8,6) * 1 * (-3)^6 * x^6. Simplifying further, we get C(8,6) * 729 * x^6.
The binomial coefficient C(8,6) can be calculated as 8! / (6! * 2!) = 8 * 7 / 2 = 28.
Therefore, the coefficient of x^6 in (1-3x)^8 is 28 * 729 = 20412.Rate this question:
-
- 10.
Find the coefficient of x^3 in the expansion of (3-4x)(2-x/2)^7
- A.
435
- B.
-882
- C.
632
Correct Answer
B. -882Explanation
To find the coefficient of x^3 in the expansion of (3-4x)(2-x/2)^7, we can use the binomial theorem. The binomial theorem states that the coefficient of x^k in the expansion of (a+b)^n is given by the formula: C(n, k) * a^(n-k) * b^k. In this case, a = 3-4x, b = 2-x/2, n = 7, and k = 3. Plugging these values into the formula, we get: C(7, 3) * (3-4x)^(7-3) * (2-x/2)^3. Simplifying further, we get: C(7, 3) * (3-4x)^4 * (2-x/2)^3. The coefficient of x^3 is the coefficient of x in this expression, which is -882.Rate this question:
-
- 11.
With the help of this binomial theorem for positive integral index indices , we can expand any power of x + y into a sum of terms forming a polynomial.
- A.
True
- B.
False
Correct Answer
A. TrueExplanation
The binomial theorem states that for any positive integral index, we can expand any power of x + y into a sum of terms forming a polynomial. This means that we can express expressions like (x + y)^n as a polynomial with multiple terms. Therefore, the statement "With the help of this binomial theorem for positive integral index indices, we can expand any power of x + y into a sum of terms forming a polynomial" is true.Rate this question:
-
- 12.
Find the coefficients of x^2 in the expansion of (1-2x)^5.23
- A.
23
- B.
40
- C.
51
Correct Answer
B. 40Explanation
To find the coefficient of x^2 in the expansion of (1-2x)^5.23, we can use the binomial theorem. The general term of the expansion is given by (5.23Ck) * (1)^k * (-2x)^(5.23-k), where k is the power of x. To find the coefficient of x^2, we need to find the value of k for which (5.23-k) = 2. Solving this equation, we get k = 3.23. Plugging this value into the general term, we get (5.23C3.23) * (1)^3.23 * (-2x)^(5.23-3.23). Simplifying further, we get (5.23C3.23) * (-8x^2). Using the binomial coefficient formula, we find that (5.23C3.23) = 40. Therefore, the coefficient of x^2 is 40.Rate this question:
-
Quiz Review Timeline +
Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.
-
Current Version
-
Mar 22, 2023Quiz Edited by
ProProfs Editorial Team -
Feb 11, 2011Quiz Created by
Yuheng222
What Celebrity Do I Look Like Quiz? Discover Your Celebrity Look Alike
What Celebrity Do I Look Like Quiz? Discover Your Celebrity Look Alike
JoJo's Bizarre Adventure: Which Jojo Stand Do You Have
JoJo's Bizarre Adventure: Which Jojo Stand Do You Have
Back to top