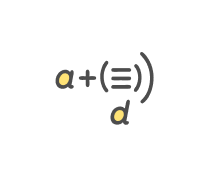9106 Number Patterns First 3 Terms Given A & D
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
Submit
×
Thank you for your feedback!