General Term Of Transformations Quiz

In the study of mathematics, a transformation is a general term given to four specific ways of manipulating the shape of a point, line, or shape. Can you answer the following questions regarding transformation? Let’s find out.
- 1.
Use arrow notation (-->) to write a rule for the following transformation: right 7 units and down 8 units.
Explanation
The given answer correctly uses arrow notation to describe the transformation. It states that for any point (x, y), the transformation involves moving 7 units to the right (increasing the x-coordinate by 7) and 8 units down (decreasing the y-coordinate by 8). This rule accurately represents the given transformation.Rate this question:
- 2.
Use arrow notation (-->) to write a rule for the following transformation: left 5 units and down 6 units.
Explanation
The given answer correctly uses arrow notation to describe the transformation. The rule states that for any point (x, y), the new point will be obtained by subtracting 5 from the x-coordinate and subtracting 6 from the y-coordinate. This represents a movement of 5 units to the left and 6 units down from the original point.Rate this question:
- 3.
The following graph is an example of what transformation?
Explanation
The given answer states that the graph is an example of a reflection. A reflection is a transformation that flips a figure over a line, creating a mirror image. However, the question is incomplete and does not provide any information about the graph or the transformation being performed. Therefore, a proper explanation cannot be generated.Rate this question:
- 4.
What is this figure's angle of rotation? (Answer in the following form: "___ degrees", include "degrees" in your answer!)
Explanation
The figure's angle of rotation is 90 degrees. The answer is given in two forms, "90 degrees" and "90 Degrees", both of which indicate that the figure has been rotated by an angle of 90 degrees.Rate this question:
- 5.
What is this figure's angle of rotation? (Answer in the following form: "___ degrees", include "degrees" in your answer!)
Explanation
The figure's angle of rotation is 45 degrees.Rate this question:
- 6.
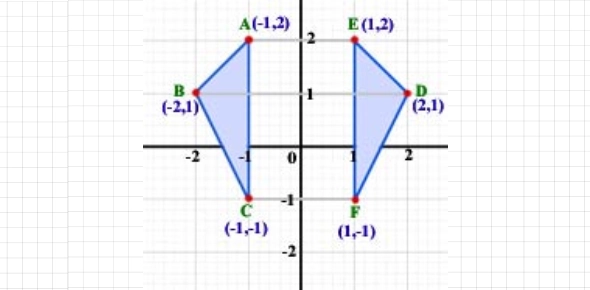
The following graph is an example of what transformation?
Explanation
The given graph is an example of a rotation transformation. A rotation transformation involves rotating an object around a fixed point by a certain angle. In this case, the graph has been rotated, as indicated by the word "rotation" being mentioned twice in the answer. However, without further information or a visual representation of the graph, it is not possible to provide a more specific explanation of the transformation.Rate this question:
- 7.
The following graph is an example of what transformation?
Explanation
The graph is an example of a translation. This is evident from the fact that the graph has shifted from its original position without any change in shape or size. The term "translation" refers to the movement of an object without any rotation or reflection. Therefore, the correct answer is translation.Rate this question:
- 8.
A change in the position, size or shape of a figure.
- A.
Image
- B.
Translation
- C.
Transformation
- D.
Reflection
Correct Answer
C. TransformationExplanation
Transformation is the correct answer because it refers to a change in the position, size, or shape of a figure. This term encompasses various types of transformations, such as translation, rotation, reflection, and dilation. These transformations can be applied to both 2D and 3D figures, altering their appearance while preserving certain properties, such as angles or distances.Rate this question:
-
- 9.
To move each point of a figure the same distance and the same direction.
- A.
Pre-image
- B.
Image
- C.
Translation
- D.
Transformation
Correct Answer
C. TranslationExplanation
Translation is the correct answer because it refers to the process of moving each point of a figure the same distance and in the same direction. This transformation does not change the shape or orientation of the figure, but simply shifts it to a different location in the coordinate plane.Rate this question:
-
- 10.
The figure you start with.
- A.
Image
- B.
Translation
- C.
Pre-Image
- D.
Transformation
Correct Answer
C. Pre-ImageExplanation
The term "pre-image" refers to the original figure or shape before any transformations have been applied to it. In this context, the correct answer suggests that the figure being referred to is the one that you start with before any transformations are made.Rate this question:
-
- 11.
The figure you get after a transformation has been performed.
- A.
Image
- B.
Pre-Image
- C.
Transformation
- D.
Translation
Correct Answer
A. ImageExplanation
The term "image" refers to the figure that is obtained after a transformation has been performed. In this context, a transformation could refer to any type of geometric transformation such as translation, rotation, reflection, or dilation. The image is the resulting figure that is obtained after applying the transformation to the original figure, known as the pre-image.Rate this question:
-
- 12.
Translating a point up and down affects the ______.
- A.
X-coordinate
- B.
Y-coordinate
Correct Answer
B. Y-coordinateExplanation
Translating a point up and down means moving it vertically along the y-axis. This movement only affects the y-coordinate of the point, as the x-coordinate remains unchanged. Therefore, the correct answer is the y-coordinate.Rate this question:
-
- 13.
Translating a point left and right affects the ______.
- A.
X-coordinate
- B.
Y-coordinate
Correct Answer
A. X-coordinateExplanation
Translating a point left and right affects the x-coordinate. When a point is translated left or right, its x-coordinate changes while its y-coordinate remains the same. This is because the x-coordinate represents the horizontal position of the point on a coordinate plane, while the y-coordinate represents the vertical position. Therefore, moving a point left or right will only affect its x-coordinate.Rate this question:
-
- 14.
A figure has a __________ if it can be roatated 80 degrees or less and matches the original figure 360/# of lines of symmetry.
- A.
Rotational Symmetry
- B.
Reflectional Symmetry
- C.
Line of Symmetry
- D.
Reflection
Correct Answer
A. Rotational SymmetryExplanation
A figure has rotational symmetry if it can be rotated 80 degrees or less and still match the original figure when rotated a total of 360 divided by the number of lines of symmetry.Rate this question:
-
- 15.
A transformation that turns a figure about a fixed point.
- A.
Reflection
- B.
Rotation
- C.
Translation
- D.
Rotational Symmetry
Correct Answer
B. RotationExplanation
Rotation is the correct answer because it is a transformation that turns a figure about a fixed point. When a figure is rotated, it is moved in a circular motion around a central point, while maintaining its shape and size. This transformation is commonly used in geometry to describe the movement of objects in a plane.Rate this question:
-
- 16.
The fixed point where the figure rotates around.
- A.
Rotation
- B.
Reflection
- C.
Reflectional Symmetry
- D.
Center of Rotation
Correct Answer
D. Center of RotationExplanation
The correct answer is "Center of Rotation." This refers to the fixed point around which a figure rotates. It is the point that remains stationary while the rest of the figure moves in a circular motion.Rate this question:
-
- 17.
The number of degrees a figure rotates.
- A.
Rotation
- B.
Rotational Degree
- C.
Angle of Rotation
- D.
Line of Symmetry
Correct Answer
C. Angle of RotationExplanation
Angle of rotation refers to the measure of the amount of rotation that a figure undergoes around a fixed point. It is typically measured in degrees and represents the extent to which the figure has been turned. The angle of rotation can be positive or negative, depending on the direction of rotation. This term is commonly used in geometry and is used to describe the rotational transformation of shapes.Rate this question:
-
- 18.
A transformation that flips a figure over the line of reflection.
- A.
Reflection
- B.
Rotational Symmetry
- C.
Rotation
- D.
Reflectional Symmetry
Correct Answer
A. ReflectionExplanation
A reflection is a transformation that flips a figure over a line of reflection. It creates a mirror image of the original figure.Rate this question:
-
- 19.
The line across where the figure is reflected.
- A.
Line of Symmetry
- B.
Reflectional Symmetry
- C.
Reflection
- D.
Rotational Symmetry
Correct Answer
A. Line of SymmetryExplanation
The correct answer is "Line of Symmetry." In geometry, the line of symmetry is an imaginary line that divides a figure into two identical halves. It is the line across which the figure is reflected or mirrored.Rate this question:
-
- 20.
A figure can be reflected over a line that passes through the figure so the image matches the preimage.
- A.
Line of Symmetry
- B.
Symmetry
- C.
Reflectional Symmetry
- D.
Rotational Symmetry
Correct Answer
C. Reflectional SymmetryExplanation
Reflectional symmetry refers to the property of a figure being able to be reflected over a line (known as the line of symmetry) so that the resulting image matches the original figure. This means that if a figure has reflectional symmetry, it can be divided into two equal parts by the line of symmetry, and one part can be flipped or reflected to match the other part exactly. In other words, the figure remains unchanged when reflected over the line of symmetry.Rate this question:
-
Quiz Review Timeline +
Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.
-
Current Version
-
Aug 28, 2024Quiz Edited by
ProProfs Editorial Team -
Sep 23, 2011Quiz Created by
Paige_Bee
 Back to top
Back to top



.webp)
