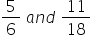Decimals, Fractions, and Equivalents: Conversions and Comparisons

Have you ever been at a supermarket trying to figure out discounts quickly? Decimals, fractions, and decimal equivalents can seem daunting initially, especially under pressure. This lesson, Decimals Fractions and Decimal Equivalents, helps resolve everyday confusion by clearly explaining these critical mathematical relationships, empowering your real-life decision-making and mathematical confidence.

What Is the Importance of Place Value in Decimals?

Understanding place value is crucial for accurately interpreting and manipulating decimal numbers. This section explains the concept of decimal place value and the significance of each digit in different decimal places.

Decimals are structured around the decimal point. Each digit's value depends on its distance from this point. Here's a scientific breakdown:

• Ones (1): Immediate left of the decimal.
• Tenths (1/10): First right digit after the decimal.
• Hundredths (1/100): Second digit after the decimal.
• Thousandths (1/1000): Third digit after the decimal.

Example: In 2.5263:

• 2 is in the one place.
• 5 is in the tenths place (0.5).
• 2 is in the hundredths place (0.02).
• 6 is in the thousandth place (0.006).
• 3 is in the ten-thousandth place (0.0003).

Place values are critical in precision tasks like scientific experiments, where even slight miscalculations can lead to significant errors.

How Do You Convert Fractions to Decimals Using a Calculator?

Decimals fractions and decimal equivalents conversions are crucial for accuracy in computations. Using calculators for conversions from fractions to decimals ensures efficiency and accuracy.

Conversion Steps:

1. Enter the numerator (top number).
2. Press the division key (/).
3. Enter the denominator (bottom number).
4. Press equals (=).

Scientific Example:

• 3/4 converts to 0.75 (3 divided by 4).
• 19/25 converts to 0.76.
• 98/100 converts to 0.98.

These decimal equivalents are essential in scientific measurements, statistical analyses, and financial calculations, providing precise and universally understandable data.

How Can Decimals Be Converted to Fractions?

Decimals fractions and decimal equivalents also encompass converting decimals back into fractions, offering clarity in conceptual understanding and simplifying numerical computations.

Conversion Steps:

1. Write the decimal as a fraction with a denominator based on the place value.
2. Simplify the fraction by dividing the numerator and denominator by their greatest common divisor.

Examples:

• 0.75 = 75/100 = 3/4
• 0.5 = 5/10 = 1/2
• 0.125 = 125/1000 = 1/8

Such conversions are frequently used in engineering and carpentry to maintain precision in measurements and ensure accuracy in design and implementation.

Why Is Comparing and Ordering Decimals and Fractions Important?

Accurately comparing and ordering decimals and fractions are fundamental for data organization, interpretation, and analysis.

Steps for Comparison:

• Convert fractions to decimals or decimals to fractions.
• Compare based on numerical value.
• Order accordingly.

Example:

• 3.1 compared with 3 1/2 (converted to 3.5): clearly, 3.1 < 3.5.
• Ordering 7.3, 7 1/2 (7.5), 7.03, 7.33 becomes 7.03, 7.3, 7.33, 7.5.

Comparisons help organize data effectively in scientific research, statistics, and economic reports.

Take This Quiz!

Exam: Skill #41- Comparing and Ordering Fractions

How Can You Express Decimals in Expanded and Word Forms?

Expanded word forms demystify decimals fractions and decimal equivalents by explicitly illustrating each digit's value, improving comprehension and facilitating error detection.

Expanded Form: Breaks down the decimal by place value.

• Example: 2.05 becomes 2 + 0.05.

Word Form: Converts decimals into words.

• Example: 2.05 = "Two and five hundredths."

Such clear representations are invaluable in technical writing, ensuring clarity and precision in documentation.

What Role Do Patterns in Decimals Play?

Recognizing patterns in decimal sequences can significantly enhance problem-solving efficiency, predictive accuracy, and strategic planning.

Example Pattern:

• 3.1, 6.2, 9.3, ____, 15.5.
• Each increases by 3.1, hence, the missing number is 12.4.

Understanding decimal patterns supports scientific forecasting and financial trend analyses, allowing for precise future predictions.

How Does Decimal Understanding Apply in Geometry?

Decimals fractions and decimal equivalents are practically applied in geometry, notably in calculating perimeters and areas, which are critical for accurate construction and design.

Perimeter Calculation:

• Rectangle perimeter formula: P = 2(l + w).
• Example: Rectangle of length 7 cm, width 12 cm:
  • P = 2(7 + 12) = 38 cm.

Accurate decimal calculations are essential for engineering, architecture, and various fields that rely on precise spatial measurements.

What Techniques Improve Accuracy in the Addition and Subtraction of Decimals?

Accurate addition and subtraction of decimals are vital in mathematics and science, demanding careful alignment and attention to place values.

Key Steps:

1. Align the decimals vertically based on the decimal point.
2. Add or subtract column-wise from right to left.

Examples:

• 23.78 + 5.62 = 29.40.
• 52.6 + 96,890.95 = 96,943.55.
• 17.12 - 0.6 = 16.52.

Precision in decimal calculations ensures correct budgeting, accurate scientific measurements, and reliable data analysis.

Practice Problems and Deep Analysis

To fully grasp decimals, fractions, and decimal equivalents, active problem-solving is essential. Practicing varied problems with detailed explanations solidifies understanding and prepares you thoroughly for assessments and real-life scenarios.

Examples to Practice:

• Convert complex fractions like 7/16 and 5/8 into decimals.
• Compare decimals like 0.203, 0.23, 0.032 and order them accurately.
• Calculate perimeters using decimal measurements and verify the importance of accuracy.

Take This Quiz!

Decimals Fractions and Decimal Equivalents quiz