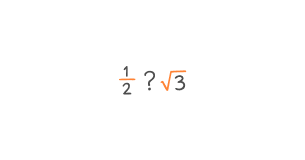Rational Numbers: Key Types, Properties, and Everyday Examples
Lesson Overview
Numbers are everywhere in the world around us, from counting objects to measuring distances. Similarly, knowledge of rational numbers is essential for solving problems involving fractions and decimals. This math lesson on rational numbers will help you learn how to identify numbers and understand how they work in math.
What Are Rational Numbers?
Rational numbers are simply numbers that can be written as fractions where both the top (numerator) and the bottom (denominator) are whole numbers.
Note: The denominator (the bottom number) cannot be zero because dividing by zero is not possible.
Take This Quiz :
How to Identify Rational Numbers
There are some simple rules and examples to identify rational numbers -
Example of Rational Numbers:
- Whole numbers: 5 is rational because it can be written as 5/1.
- Fractions: 3/4, 7/2, and 10/5 are all rational numbers.
- Decimals that stop or repeat: 0.5 (which is 1/2) and 0.333… (which is 1/3) are rational numbers.
Numbers That Are Not Rational:
- Numbers like the square root of 2 (√2), or π (Pi) cannot be written as fractions-they're called irrational numbers.
Types of Rational Numbers
| Type of Rational Number | Description | Examples |
| Whole Numbers | Numbers that start from 0 and include all positive numbers, with no fractions. | 0, 1, 2, 3, 4, 10 |
| Integers | Whole numbers and their negative counterparts (no fractions or decimals). | -3, -2, -1, 0, 1, 2, 3 |
| Fractions | Numbers written as a part of a whole, where the top number (numerator) is divided by the bottom number (denominator). | 1/2, 3/4, 7/10 |
| Decimals (Terminating) | Numbers with a finite number of digits after the decimal point. | 0.5, 2.75, 4.6 |
| Decimals (Repeating) | Numbers with one or more digits that repeat endlessly after the decimal point. | 0.333… (1/3), 0.666… |
Rational Number Properties:
Rational numbers have some cool properties or rules they follow.
1. Closure Property: Staying Within the Lines
- When you add or multiply two rational numbers, the answer is always another rational number. It stays within the "fraction family."
- Example: 1/2 + 1/4 = ¾
2. Commutative Property: Order Doesn't Matter
- When you add or multiply rational numbers, the order doesn't change the answer.
- Example: 1/3 + 1/2 = 1/2 + 1/3
- Example: 2/5 x 1/4 = 1/4 x ⅖
3. Associative Property:
- When adding or multiplying three or more rational numbers, it doesn't matter how you group them, the answer stays the same.
- Example: (1/4 + 1/2) + 1/3 = 1/4 + (1/2 + 1/3)
4. Additive Identity:
- Adding zero to any rational number doesn't change that number. Zero is the "additive identity."
- Example: 3/5 + 0 = ⅗
5. Multiplicative Identity: The One and Only
- Multiplying any rational number by one doesn't change that number. One is the "multiplicative identity."
- Example: 2/7 x 1 = 2/7
- Example: 2/7 x 1 = 2/7
Rational vs Irrational Numbers
This table gives a simple example of rational and irrational numbers using easy examples.
| Category | Rational Numbers | Irrational Numbers |
| What Are They? | Numbers that can be written as fractions (like a/b). | Numbers that cannot be written as simple fractions. |
| Examples | 1/2, 3/4, 7, -5, 0.75, 5.5, 0.3, 0, 4 (These can be written as fractions!) | √2, π (Pi), √3, 1.414... (They go on forever without repeating!) |
| Decimals | Decimals that either end (like 0.5) or repeat in a pattern (like 0.333…). | Decimals that go on forever without repeating or ending (like 3.14159…). |
| Can You Count Them? | Yes! You can count and list rational numbers. | No! You cannot list all irrational numbers because they go on forever without a pattern. |
| Can You Write Them as Fractions? | Yes! All rational numbers can be written as fractions. | No! Irrational numbers cannot be written as fractions. |
Take This Quiz :
Rational Numbers Example
Example 1: Add the rational numbers
3/4 and 1/2.
Solution:
- Find a common denominator.
The denominators are 4 and 2. The common denominator is 4 because it's the smallest number both 4 and 2 can divide into. - Rewrite the fractions.
We need to make 1/2 have the same denominator as 3/4.
1/2 becomes 2/4 because 1 × 2 = 2 and 2 × 2 = 4. - Now add the fractions.
3/4 + 2/4 = (3 + 2) / 4 = 5/4.
Final Answer:
5/4 is an improper fraction. You can also write it as 1 1/4 (one and one-fourth).
Example 2: Subtracting Rational Numbers
Problem:
Subtract 3/5 from 4/5.
Solution:
- Same denominator.
Since both fractions already have the same denominator (5), we can subtract the numerators. - Subtract the fractions.
4/5 - 3/5 = (4 - 3) / 5 = 1/5.
Final Answer:
The answer is 1/5.
Example 3: Multiplying Rational Numbers
Problem:
Multiply 2/3 by 3/4.
Solution:
- Multiply the numerators.
2 × 3 = 6. - Multiply the denominators.
3 × 4 = 12. - Simplify the fraction (if needed).
6/12 can be simplified to 1/2 because both 6 and 12 can be divided by 6.
Answer:
1/2.
Example 4: Dividing Rational Numbers
Problem:
Divide 5/6 by 2/3.
Solution:
- Flip the second fraction.
We flip 2/3 to get 3/2. - Multiply.
Now, multiply 5/6 by 3/2.
5 × 3 = 15, and 6 × 2 = 12. - Simplify the fraction (if needed).
15/12 can be simplified to 5/4 by dividing both the numerator and denominator by 3.
Answer:
5/4.
Rational Numbers Assessment
- Which of the following numbers is a rational number?
a) 5
b) √2
c) 1/3
d) π
- Which of these is NOT a rational number?
a) -4
b) 0.5
c) √3
d) 2/5
- Convert the following decimal into a fraction: 0.75.
- Which number is greater?
a) 3/4
b) 2/3
- True or False: The number -6 is a rational number.
Answer:
- c) 1/3
Explanation: A rational number is any number that can be written as a fraction of two integers (whole numbers), like 1/3. - c) √3
Explanation: √3 is an irrational number because it cannot be written as a fraction of two integers. - 0.75 = 3/4
Explanation: To convert 0.75 into a fraction, write it as 75/100, then simplify it by dividing both the numerator and the denominator by 25. - a) 3/4
Explanation: To compare fractions, convert them to have the same denominator. 3/4 is greater than 2/3 because 3/4 = 9/12 and 2/3 = 8/12.
- True
Explanation: -6 is a rational number because it can be written as -6/1, which is a fraction of two integers.
Rate this lesson:
 Back to top
Back to top
(390).webp)