Nonlinear Function Lesson| Definition, Examples & Graphs

Lesson Overview

• What Is a Nonlinear Function?
• Nonlinear Function Table
• Non-linear Graphs
• Nonlinear Function Equation
• How to Identify Nonlinear Functions
• Difference Between Linear and Nonlinear Functions
• Non Linear Function Examples

Nonlinear functions capture the intricate patterns and behaviors observed in various phenomena, from the growth of populations to the trajectory of a projectile. 

They provide a powerful tool for analyzing data, making predictions, and solving problems in fields ranging from physics and engineering to economics and biology.

What Is a Nonlinear Function?

A nonlinear function is a function whose graph is not a straight line. Equivalently, it does not satisfy the properties of additivity and homogeneity.

The table shows that as x increases by 1, y doubles. This pattern suggests the function is exponential, like y = 100 * 2^x.

The doubling pattern shows rapid growth, which is typical of nonlinear, especially exponential, functions.

x	y
0	100
1	200
2	400
3	800

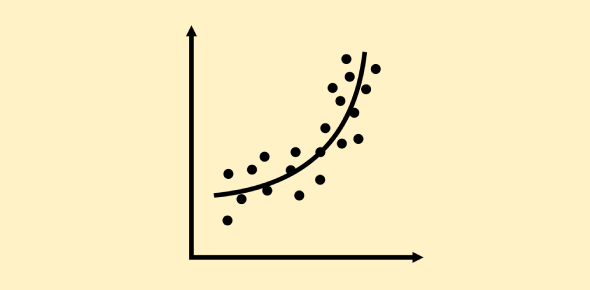
The graph shows a nonlinear function, meaning the relationship between the input x and the output y is not a straight line. This means the rate of change of y with respect to x is not constant.

The curve starts at x = 0 and increases quickly as x gets larger, which suggests exponential growth. As x increases, the output value grows faster.

The graph is a smooth curve, confirming that the function is nonlinear and not a straight line.

In conclusion, both the graph and the table show exponential growth, which is a type of nonlinear function.

Take this quiz -

Nonlinear Function Table

A nonlinear function table displays inputs (x-values) and their corresponding outputs (y-values), where the relationship between them doesn't follow a constant rate of change.

x	y
-2	5
-1	2
0	1
1	2
2	5

Non-linear Graphs

Nonlinear functions are visually represented by graphs that are not straight lines. These graphs can take various shapes, such as curves, parabolas, or hyperbolas, reflecting the non-constant rate of change in the function.

Parabolic Graph

The graph represents the function f(x) = x squared.

It is a parabola that opens upwards.

The vertex of the parabola is at the point (0, 0).

The curve is symmetrical around the y-axis.

As x moves away from 0, the values of f(x) increase in both positive and negative directions.

For example, when x is -2 or 2, the value of f(x) is 4.

Logarithmic Graph

The graph represents the function f(x) = log(x).

The curve is only defined for positive values of x.

As x approaches 0 from the right, f(x) decreases without bound (heads towards negative infinity).

The graph passes through the point (1, 0) because log(1) = 0.

For x greater than 1, the function increases slowly.

The y-axis acts as a vertical asymptote, meaning the graph gets infinitely close to the y-axis but never touches it.

Trigonometric Graph

The graph shows the function f(x) = sin(x).

It is a wave that repeats every 2π.

The values go up to 1 and down to -1, which are the highest and lowest points.

The graph crosses the x-axis at multiples of π, like -3π, -2π, -π, 0, π, 2π, and 3π.

The highest points are at π/2, 5π/2, and so on, while the lowest points are at -π/2, -5π/2, and so on.

The wave is smooth and looks the same in each cycle

Exponential Graph

The graph represents the function f(x) = 2^x.

It is an exponential curve that grows rapidly as x increases.

For x less than 0, the graph gets closer and closer to the x-axis but never touches it (the x-axis is a horizontal asymptote).

At x = 0, the value is 1 because 2^0 = 1.

As x increases, the values of f(x) rise very quickly.

The curve is smooth and always stays above the x-axis.

Take this quiz -

Nonlinear Function Equation

Nonlinear functions are represented by equations that deviate from the standard form of a linear equation (y = mx + c). 

Function Type	Example Equation	Description
Quadratic Function	y = x²	Involves a variable raised to the second power. Graphs as a parabola.
Exponential Function	y = 2^x	Variable appears in the exponent. Models rapid growth or decay.
Logarithmic Function	y = log₂(x)	Inverse of an exponential function.
Rational Function	y = (x + 1) / (x - 2)	Ratio of two polynomials. Often has asymptotes.

How to Identify Nonlinear Functions

Examine the equation: Look for exponents other than 1, variables in the denominator, or terms involving roots or radicals.

Analyze the graph: Check if the graph is a straight line. If it's curved, bent, or has discontinuities, it represents a nonlinear function.Inspect the table: If the rate of change between the input and output values is not constant, the function is nonlinear.

Difference Between Linear and Nonlinear Functions

Linear and nonlinear functions are fundamental concepts in algebra, representing distinct types of relationships between variables.

They differ primarily in how they change and how this change is visualized on a graph, represented in an equation, and revealed through a table of values.

Feature	Linear Functions	Nonlinear Functions
Graph	Straight line	Not a straight line
Equation	f(x) = ax + b	Any form except f(x) = ax + b
Slope	Constant for any two points	Changes between different pairs of points
Table	Difference in y / Difference in x = Constant	Difference in y / Difference in x ≠ Constant

Non Linear Function Examples

1. Quadratic Function

If f(x) = 2x² - 3x + 1, find f(4).

Substitute the value of x = 4 into the function: f(4) = 2(4)² - 3(4) + 1

Simplify using the order of operations (PEMDAS/BODMAS): f(4) = 2(16) - 12 + 1 f(4) = 32 - 12 + 1 f(4) = 21

2. Cubic Function

If g(x) = x³ - 2x² + 5, find g(-2).

Substitute x = -2 into the function: g(-2) = (-2)³ - 2(-2)² + 5

Simplify: g(-2) = -8 - 2(4) + 5 g(-2) = -8 - 8 + 5 g(-2) = -11

3. Exponential Function

If h(x) = 3(2^x), find h(3).

Substitute x = 3 into the function: h(3) = 3(2³)

Simplify: h(3) = 3(8) h(3) = 24

4. Absolute Value Function

If k(x) = |4x - 7| + 2, find k(-1).

Substitute x = -1 into the function: k(-1) = |4(-1) - 7| + 2

Simplify inside the absolute value first: k(-1) = |-4 - 7| + 2 k(-1) = |-11| + 2

Evaluate the absolute value (make it positive): k(-1) = 11 + 2 k(-1) = 13

5. Square Root Function

If p(x) = √(x + 5) - 1, find p(4).

Substitute x = 4 into the function: p(4) = √(4 + 5) - 1

Simplify inside the radical: p(4) = √9 - 1

Evaluate the square root: p(4) = 3 - 1 p(4) = 2

Take this quiz -