Angle Properties - Parallel Lines Quiz
(150).jpg)
Dive into the fascinating realm of geometry with our "Angle Properties - Parallel Lines Quiz." This quiz is designed to test your understanding of the relationships between angles formed by parallel lines and transversals. Challenge yourself with thought-provoking questions that explore interior angles, exterior angles, corresponding angles, and more.
Whether you're a student looking to reinforce your geometry skills or an enthusiast eager to explore the intricacies of parallel lines, this quiz offers an engaging platform. Uncover the secrets of angle properties and enhance your geometric prowess. Sharpen your knowledge in a fun and interactive way as you master the Read moreprinciples governing angles within the context of parallel lines.
- 1.
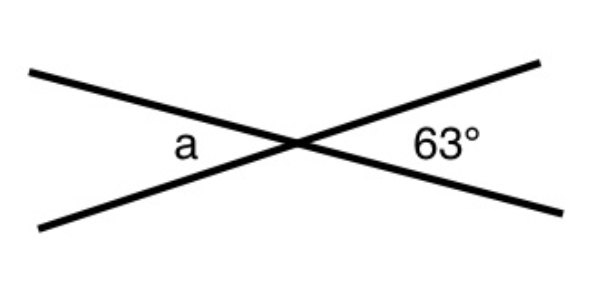
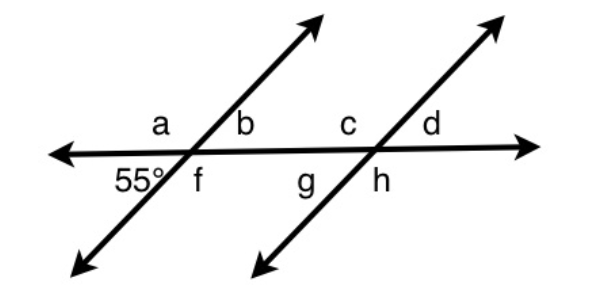
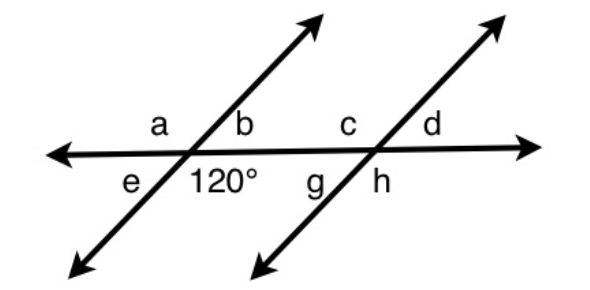
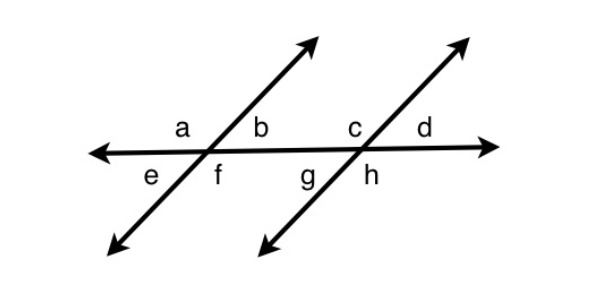
angles a and b are:
- A.
Alternate
- B.
Co-interior
- C.
Vertically-opposite
- D.
Corresponding
- E.
Exterior
Correct Answer
C. Vertically-oppositeExplanation
Vertically-opposite angles are formed when two lines intersect. In this case, angles a and b are formed by the intersection of two lines. Vertically-opposite angles are always equal to each other, meaning that angle a is equal to angle b. This is why the answer is vertically-opposite.Rate this question:
-
- 2.
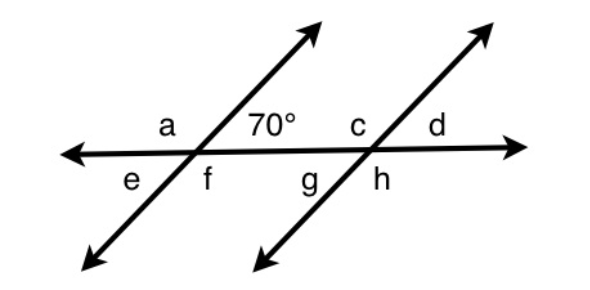
angles a and c are:
- A.
Alternate
- B.
Co-interior
- C.
Vertically-opposite
- D.
Corresponding
- E.
Exterior
Correct Answer
D. CorrespondingExplanation
Angles a and c are corresponding angles. Corresponding angles are formed when a transversal intersects two parallel lines. In this case, the angles a and c are located in the same position on the two parallel lines, one on each line. Corresponding angles have equal measures, so angle a and angle c are equal.Rate this question:
-
- 3.
angles b and c are:
- A.
Alternate
- B.
Co-interior
- C.
Vertically-opposite
- D.
Corresponding
- E.
Exterior
Correct Answer
B. Co-interiorExplanation
Angles b and c are co-interior angles because they are located on the same side of the transversal line and on the inside of the two parallel lines. Co-interior angles are supplementary, which means that their sum is equal to 180 degrees. In this case, angles b and c add up to 180 degrees, indicating that they are co-interior angles.Rate this question:
-
- 4.
angles b and g are:
- A.
Alternate
- B.
Co-interior
- C.
Vertically-opposite
- D.
Corresponding
- E.
Exterior
Correct Answer
A. AlternateExplanation
Angles b and g are alternate angles. Alternate angles are formed when a transversal intersects two parallel lines. In this case, the angles b and g are on opposite sides of the transversal and on different parallel lines. Alternate angles are congruent, meaning they have the same measure.Rate this question:
-
- 5.
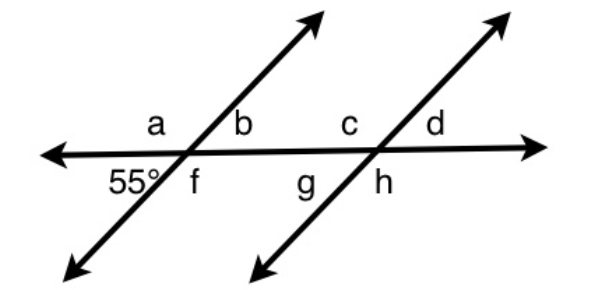
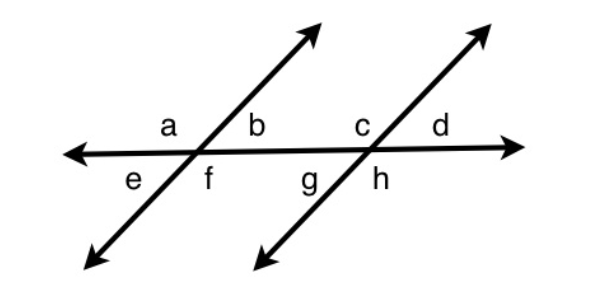
How many degrees is angle a?
Correct Answer
63, sixty three, 63 degrees, 63 degree, sixty-three degreeExplanation
The given answer "63, sixty three, sixtythree" indicates that angle a measures 63 degrees. The angles are vertical, which means they are equal to each other. Thus, if one angle is 63 degrees, then so is the other angle.Rate this question:
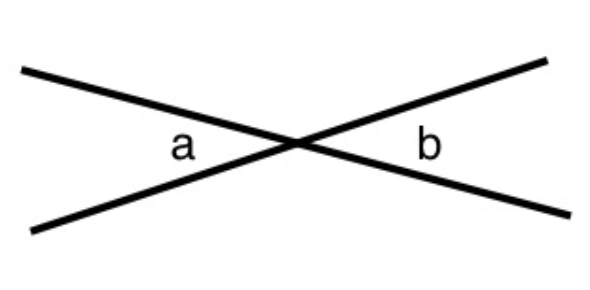
- 6.
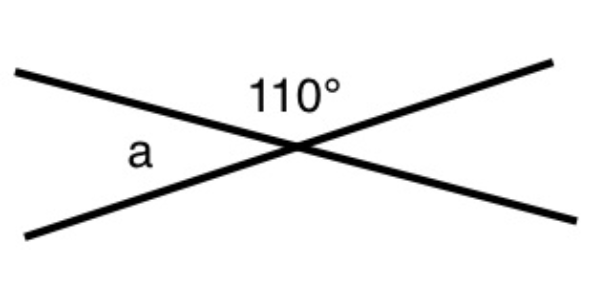
How many degrees is angle a?
Correct Answer
70, seventy - 7.
How many degrees is angle c?
Correct Answer
110, one hundred and ten, one hundred tenExplanation
70 degrees and angle “c” are co-interior angles. They add up to equal 180. Thus, to determine what angle “c” is we will subtract 70 from 180, which gives us 110.Rate this question:
- 8.
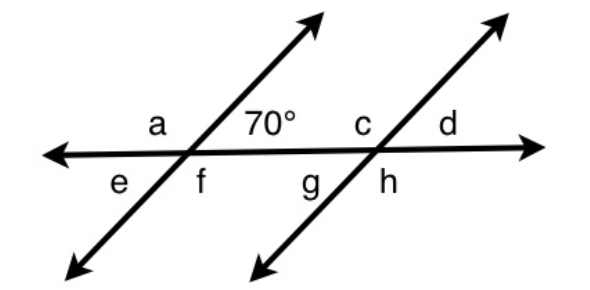
what is the size of angle g?
- A.
70°
- B.
110°
Correct Answer
A. 70°Explanation
The size of angle g is 70°. Both angles are alternate, which means they are equal to each other. Thus, angle “g” is also 70 degrees.Rate this question:
-
- 9.
How many degrees is angle g?
- A.
125
- B.
180
- C.
135
- D.
90
- E.
55
Correct Answer
E. 55Explanation
The correct answer is 55 because angle g and 55 degrees are corresponding angles, which means they are equal.Rate this question:
-
- 10.
What is the size of angle d?
- A.
55°
- B.
90°
- C.
125°
- D.
180°
- E.
25°
Correct Answer
A. 55°Explanation
The size of angle d is 55°. Angle b and 55 degrees are vertical angles, which means they are equal. Thus, angle b is 55. However, angle b and angle d are corresponding angles. Corresponding angles are equal to each other. Thus, angle d is 55.Rate this question:
-
- 11.
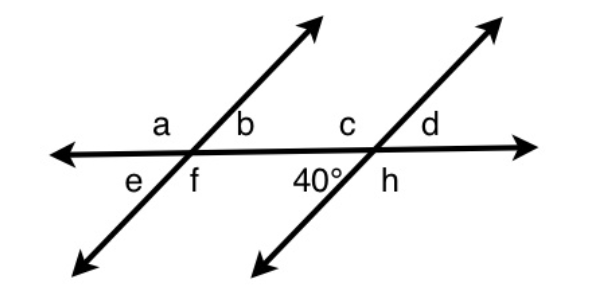
How many degrees is angle f?
Correct Answer
140, one hundred and forty, one hundred fortyExplanation
Angle f and 40 degrees are co-interior angles. Co-interior angles are supplementary which mean they add up to equal 180. Thus, we will subtract 40 from 180 to determine that angle f is 140 degrees.Rate this question:
- 12.
How many degrees is angle b?
Correct Answer
40, fortyExplanation
Angle “b” and 40 degrees are alternate angles. Alternate angles are equal to each other. Thus, angle b is also 40 degrees.Rate this question:
- 13.
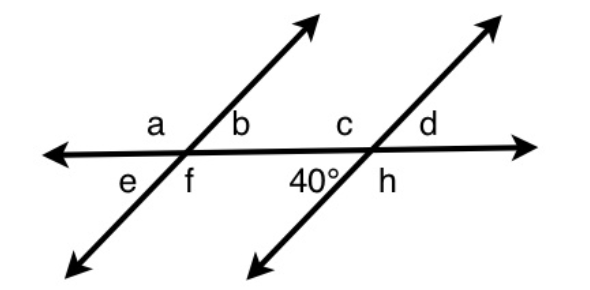
How many degrees is angle a?
- A.
180°
- B.
40°
- C.
200°
- D.
140°
- E.
50°
Correct Answer
D. 140°Explanation
Angle f and 40 degrees are co-interior angles. Co-interior angles are supplementary, which means they add up to equal 180. Thus, we will subtract 40 from 180 to determine that angle f is 140 degrees. However, angle “a” and angle “f” are vertical angles, which means they are equal. Thus, if angle f is 140, then angle “a” is also 140.Rate this question:
-
- 14.
How many degrees is angle a?
- A.
60°
- B.
120°
- C.
180°
- D.
160°
- E.
80°
Correct Answer
B. 120°Explanation
Angle “a” and 120 degrees are vertical angles, which means they are equal. Thus, angle “a” is also 120.Rate this question:
-
- 15.
How many degrees is angle c?
Correct Answer
120, one hundred and twenty, one hundred twentyExplanation
Angle “c” and 120 degrees are alternate angles, which means they are equal. Thus, angle “c” is also 120.Rate this question:
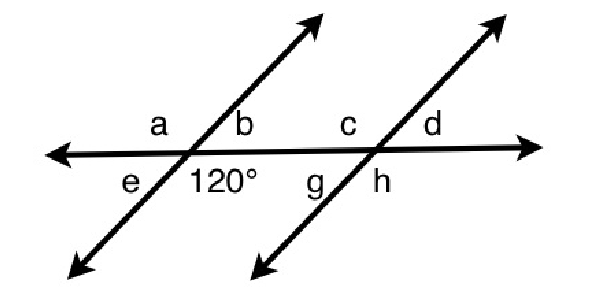
- 16.
How many degrees is angle d?
Correct Answer
60, sixtyExplanation
Identify the relationships between the angles:
The angles marked 120° and 'e' are supplementary angles (they add up to 180°).
Angles 'e' and 'd' are alternate interior angles. Alternate interior angles are formed when a transversal line intersects two parallel lines. They are located on opposite sides of the transversal and inside the parallel lines.
2. Find the measure of angle 'e':
Since the 120° angle and angle 'e' are supplementary:
e + 120° = 180° e = 60°
3. Find the measure of angle 'd':
When a transversal intersects two parallel lines, alternate interior angles are congruent (equal). Therefore:
d = e d = 60°
Therefore, angle d measures 60°.Rate this question:
Quiz Review Timeline +
Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.
-
Current Version
-
Jan 13, 2025Quiz Edited by
ProProfs Editorial Team
Expert Reviewed by
Janaisa Harris -
Aug 17, 2010Quiz Created by
Joel Dodd
 Back to top
Back to top



.webp)