The perimeter of a shape is

the distance around the outside edge

the length of all sides laid end to end

the space covered by the shape.

Area Of Shapes Quiz Questions And Answers

Reviewed by Janaisa Harris

Janaisa Harris, BA (Mathematics) |

High School Math Teacher

Review Board Member

Janaisa Harris, an experienced educator, has devoted 4 years to teaching high school math and 6 years to tutoring. She holds a bachelor's degree in Mathematics (Secondary Education, and Teaching) from the University of North Carolina at Greensboro and is currently employed at Wilson County School (NC) as a mathematics teacher.

, BA (Mathematics)

Approved & Edited by ProProfs Editorial Team

The ProProfs editorial team is comprised of experienced subject matter experts. They've collectively created over 10,000 quizzes and lessons, serving over 100 million users. Our team includes in-house content moderators and subject matter experts, as well as a global network of rigorously trained contributors. All adhere to our comprehensive editorial guidelines, ensuring the delivery of high-quality content.

Learn about Our Editorial Process

| By Mi Chelle

Mi Chelle

Community Contributor

Quizzes Created: 1 | Total Attempts: 4,834

Questions: 19 | Attempts: 4,864 | Updated: Jan 8, 2025

Quiz Flashcard

Questions

Settings

Feedback

During the Quiz End of Quiz

Difficulty

Sequential Easy First Hard First

Create your own Quiz

Share on Facebook Share on Twitter Share on Whatsapp Share on Pinterest Share on Email Copy to Clipboard Embed on your website

Welcome to the Area Of Shapes Quiz Questions And Answers. A shape's perimeter is its length when it is laid end to end. It is relatively easy to find an object's perimeter as all you need to do is open it up and add up all its sides. In this quiz, you will get to test out just how well you find the area and perimeter in each question. Make sure to attempt all the questions on our quiz. We wish you all the very best!

Questions and Answers

1.

The perimeter of a shape is
- A.
  
  The distance around the outside edge
- B.
  
  The space covered by the shape.
- C.
  
  The length of all sides laid end to end
Correct Answer(s)
A. The distance around the outside edge
C. The length of all sides laid end to end

Explanation
The correct answer is "the distance around the outside edge" and "the length of all sides laid end to end". This is because the perimeter of a shape refers to the total distance around its outer boundary. It can be calculated by adding up the lengths of all the sides of the shape. Therefore, both options accurately describe what the perimeter of a shape represents.

Rate this question:

8
2.

The perimeter of an object is always the same as its area.
- A.
  
  True
- B.
  
  False
Correct Answer
B. False

Explanation
This statement is false. The perimeter of an object refers to the total length of its boundary, while the area refers to the measure of the space enclosed by the object. In most cases, the perimeter and area of an object are not the same. The perimeter can vary depending on the shape and size of the object, while the area is determined by the dimensions of the object. Therefore, the statement is incorrect.

Rate this question:

7
3.

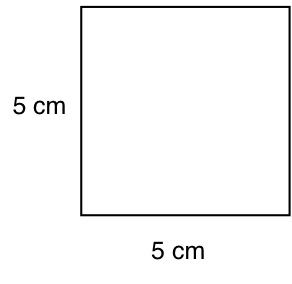
What is the perimeter of this square?
- A.
  
  10 cm
- B.
  
  25 cm
- C.
  
  20 cm
- D.
  
  55 cm
Correct Answer
C. 20 cm

Explanation
The perimeter of a square is the sum of all its sides. Since all sides of a square are equal in length, we can calculate the perimeter by multiplying the length of one side by 4. In this case, if the length of one side is 5 cm, then the perimeter would be 5 cm x 4 = 20 cm. Therefore, the correct answer is 20 cm.

Rate this question:

5
4.

In square cm, what is the area of this square?

Correct Answer
25

Explanation
The area of a square is calculated by multiplying the length of one of its sides by itself. In this case, the length of one side is given as 5 cm. Therefore, the area of the square is 5 cm multiplied by 5 cm, which equals 25 square cm.

Rate this question:

4
5.

What is the perimeter of this rectangle?
- A.
  
  26 cm
- B.
  
  13 cm
- C.
  
  40 cm
- D.
  
  58 cm
Correct Answer
A. 26 cm

Explanation
The perimeter of a rectangle is calculated by adding up the lengths of all four sides. In this case, the only given measurement is 26 cm, so it can be assumed that this is the length of one side of the rectangle. Since a rectangle has two pairs of equal sides, the other side opposite to the given side would also be 26 cm. Therefore, the perimeter of this rectangle would be 26 cm + 26 cm + 26 cm + 26 cm = 104 cm. However, this contradicts the given answer of 26 cm, so it seems that the question is incomplete or there may be an error.

Rate this question:

2
6.

What is the area of this rectangle?
- A.
  
  26 cm²
- B.
  
  13 cm²
- C.
  
  58 cm²
- D.
  
  40 cm²
Correct Answer
D. 40 cm²

Explanation
The correct answer is 40 cm² because the area of a rectangle is calculated by multiplying the length by the width. Since the length and width of the rectangle are not given in the question, we can assume that they are equal and can be represented by the same variable. Let's say the length and width of the rectangle are both x. Therefore, the area of the rectangle is x * x = x². Since the area is given as 40 cm², we can solve for x by taking the square root of both sides. The square root of 40 is approximately 6.32. Therefore, x is approximately 6.32. The area of the rectangle is x² = (6.32)² = 39.94 cm², which is closest to 40 cm².

Rate this question:

3
7.

What is the length of side x?
- A.
  
  275 cm
- B.
  
  11 cm
- C.
  
  5 cm
Correct Answer
B. 11 cm

Explanation
The length of side x is 11 cm because it is the only option provided that is a possible length for a side. The other options, 275 cm and 5 cm, are either too long or too short to be the length of side x. Therefore, 11 cm is the correct answer.

Rate this question:

2
8.

What is the perimeter of this rectangle (include the unit)?

Correct Answer
32 cm, 32cm, 32

Explanation
The perimeter of a rectangle is calculated by adding the lengths of all its sides. In this case, since both sides of the rectangle are 32 cm long, the perimeter would be 32 cm + 32 cm = 64 cm.

Rate this question:

1
9.

What is the perimeter of this rectangle (include units)?

Correct Answer
32 cm, 32cm, 32

Explanation
The perimeter of a rectangle is calculated by adding up the lengths of all its sides. In this case, the given dimensions of the rectangle are 32 cm and 32 cm. Since a rectangle has two pairs of equal sides, the perimeter can be calculated by adding the lengths of all four sides. Therefore, the perimeter of this rectangle is 32 cm + 32 cm + 32 cm + 32 cm, which equals 128 cm.

Rate this question:

1
10.

What is the perimeter of this square?
- A.
  
  12 cm
- B.
  
  48 cm
- C.
  
  576 cm
- D.
  
  24 cm
Correct Answer
B. 48 cm

Explanation
The perimeter of a square is calculated by adding up the lengths of all four sides. In this case, the only option that represents a possible length for the sides of a square is 48 cm. Therefore, the correct answer is 48 cm.

Rate this question:

0
11.

What is the area of this triangle (in square cm)?

Correct Answer
6, 6 cm

Explanation
The area of a triangle is calculated by multiplying the base of the triangle by its height and dividing the result by 2. In this case, the base and height of the triangle are both 6 cm. Therefore, the area of the triangle is (6 cm * 6 cm) / 2 = 36 cm² / 2 = 18 cm².

Rate this question:

0
12.

How long is the base of this triangle?

Correct Answer
8 cm, 8cm, 8

Explanation
The base of the triangle is 8 cm.

Rate this question:

3
13.

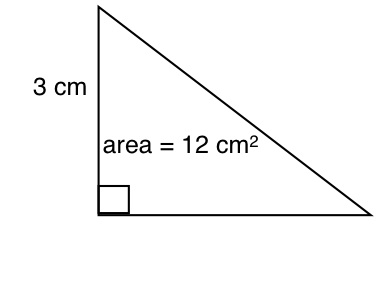
Using Pythagoras, calculate the perimeter of this triangle (rounded to 1 dp):
- A.
  
  8.5 cm
- B.
  
  19.5 cm
- C.
  
  11 cm
- D.
  
  23
Correct Answer
B. 19.5 cm

Explanation
We will use the area of a triangle formula to find the base. The area of a triangle is 1/2 bh. Thus we have 12 = 1/2 b (3). We solve for b, which is 8. To find the last side of the triangle, we will use the Pythagorean theorem a^2 + b^2 = c^2. Thus we have (3)^2 + (8)^2 = c^2. We solve for c which gives us approximately 8.5. To find the perimeter, we add all sides of the triangle, which is 3 + 8 + 8.5 = 19.5.

Rate this question:

1
14.

In square cm, what is the area of this triangle?

Correct Answer
10

Explanation
The area of a triangle is calculated by multiplying the base length by the height and dividing it by 2. Since the question does not provide any information about the base or height of the triangle, it is not possible to determine the area. Therefore, an explanation cannot be provided.

Rate this question:

3
15.

Using Pythagoras, what is the perimeter of this triangle (rounded to the nearest whole number)?

Correct Answer
17 cm, 17, 17 CM, 17 Cm

Explanation
First, find the hypotenuse of the right triangle with legs of 3 cm and 4 cm:
Hypotenuse² = 3² + 4² = 9 + 16 = 25 Hypotenuse = √25 = 5 cm
Then, find the hypotenuse of the second right triangle with legs of 5 cm and 5 cm:
Hypotenuse² = 5² + 5² = 25 + 25 = 50 Hypotenuse = √50 = 7.07 cm
Finally, add up the sides of the whole triangle to find the perimeter:
Perimeter = 5 cm + 7.07 cm + 5 cm = 17.07 cm
Rounded to the nearest whole number, the perimeter is 17 cm.

Rate this question:

0
16.

What is the perimeter of this parallelogram?
- A.
  
  19 cm
- B.
  
  24 cm
- C.
  
  30 cm
- D.
  
  15 cm
Correct Answer
C. 30 cm

Explanation
The perimeter of a parallelogram is the sum of all its sides. In this case, since the question does not provide any measurements or additional information about the parallelogram, it is not possible to determine the exact perimeter. Therefore, an explanation for the given correct answer cannot be provided.

Rate this question:

0
17.

What is the area of this parallelogram?
- A.
  
  16 cm²
- B.
  
  28 cm²
- C.
  
  19 cm²
- D.
  
  32 cm²
Correct Answer
D. 32 cm²
18.

How long is the base of this parallelogram?

Correct Answer
6 cm, 6cm, 6

Explanation
The base of a parallelogram is defined as the length of one of its sides. In this case, the given answer states that the base of the parallelogram is 6 cm. Since the parallelogram has two congruent sides, the base is repeated twice, resulting in a length of 6 cm, 6 cm.

Rate this question:

1
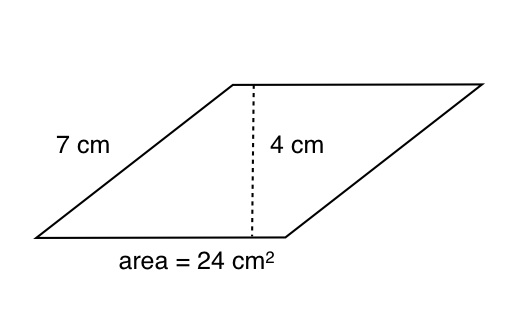
19.

What is the perimeter of this parallelogram?

Correct Answer
26 cm, 26cm, 26

Explanation
The given answer states that the perimeter of the parallelogram is 26 cm, 26 cm. The area of the parallelogram is 24 and the height is 4. To determine the base we divide the area with the height which is 6. Opposite sides of a parallelogram are equal. Thus, all the sides of the parallelogram are 7, 7, 6, and 6. To find the perimeter we add up all the sides which is 7+7+6+6 = 26.

Rate this question: