Test On Euler And Hamilton Paths And Circuits
(579).jpg "Test On Euler And Hamilton Paths And Circuits - Quiz")
Test your knowledge of Euler and Hamilton Paths and Circuits with this amazing quiz and determine whether a graph has an Euler or a Hamilton path. An Euler path is a path in a graph that uses every edge exactly one time, and it starts and ends at different vertices. A Hamilton path is a path in a graph that uses every vertex exactly once, and it begins and ends at the same vertex. The below quiz is based on Euler and Hamilton paths and/or circuits. Play it now and check your scores. Good luck!
- 1.
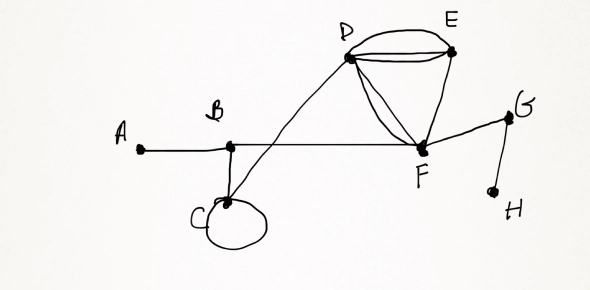
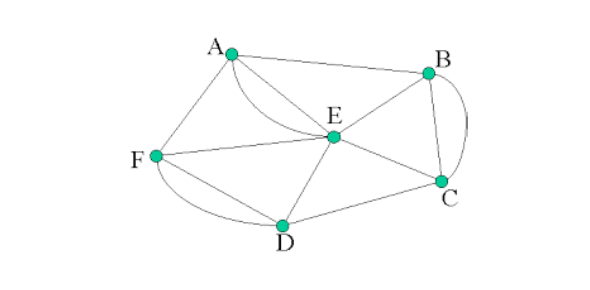
Use the above graph. The degree of Vertex C is:
Explanation
From the graph provided, we observe that Vertex C has the following edges connected to it:
Edge from C to B
Edge from C to F
Thus, Vertex C has two edges incident to it.
Therefore, the degree of Vertex C is 2.Rate this question:
- 2.
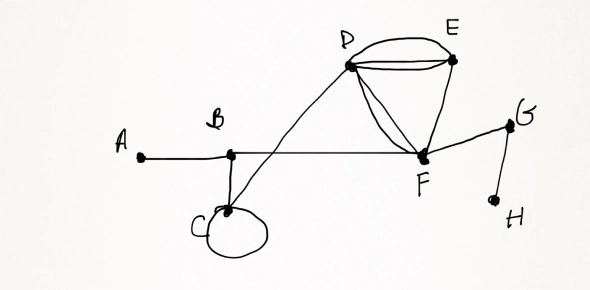
Refer to the above graph and choose the best answer:
- A.
Euler path and Euler circuit
- B.
Euler path only
- C.
Euler circuit only
- D.
Neither an Euler path nor Euler circuit
Correct Answer
A. Euler path and Euler circuitExplanation
Based on the given graph, an Euler path is a path that visits every edge exactly once, while an Euler circuit is a path that visits every edge and returns to the starting point. The graph in the question has multiple paths that visit every edge exactly once, indicating the presence of an Euler path. Additionally, the graph also has a cycle that visits every edge and returns to the starting point, indicating the presence of an Euler circuit. Therefore, the correct answer is "Euler path and Euler circuit."Rate this question:
-
- 3.
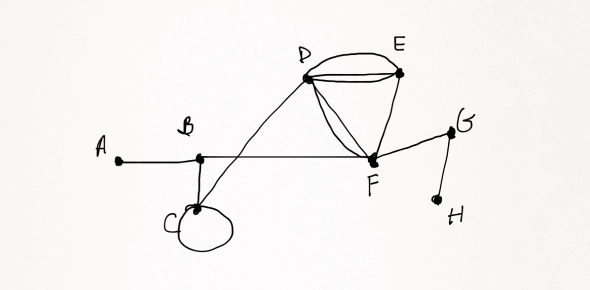
Refer to the above graph and choose the best answer:
- A.
Hamiltonian path only
- B.
Hamiltonian circuit only
- C.
Hamiltonian path and Hamiltonian circuit
- D.
Neither a Hamiltonian path nor a Hamiltonian circuit
Correct Answer
A. Hamiltonian path onlyExplanation
Based on the given graph, a Hamiltonian path is possible as it is a path that visits each vertex exactly once. However, a Hamiltonian circuit is not possible as it is a closed path that visits each vertex exactly once and returns to the starting vertex. Therefore, the correct answer is the Hamiltonian path only.Rate this question:
-
- 4.
Roberta wants to deliver the mail. She begins at the Post Office where she picks up the mail each day, but wants to end close to her home. She only wants to go down each street once. Her home is 5 miles from the Post Office. Which graph would best meet this scenario?
- A.
Euler path
- B.
Euler circuit
- C.
Hamiltonian path
- D.
Hamiltonian circuit
Correct Answer
A. Euler pathExplanation
An Euler path is a path in a graph that visits every edge exactly once. In this scenario, Roberta wants to go down each street once, which aligns with the concept of visiting each edge exactly once. Therefore, an Euler path would best meet this scenario.Rate this question:
-
- 5.
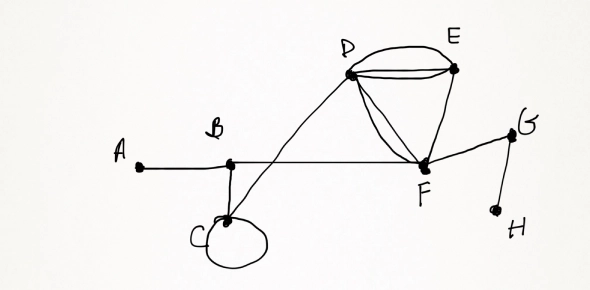
List the vertices in the above graph:
- A.
{A,B,C,D,E,F,G,H}
- B.
{A,B,F,G,H}
- C.
{D,E}
- D.
{F,G,H}
Correct Answer
A. {A,B,C,D,E,F,G,H}Explanation
The correct answer includes all the vertices in the given graph. The graph is not explicitly shown, but the answer {A,B,C,D,E,F,G,H} suggests that these are all the vertices present in the graph.Rate this question:
-
- 6.
A city is planning their snow plow route for next winter. They want to begin at the garage, go down each street only once, and end at the garage. Which graph would be best for this scenario?
- A.
Euler circuit
- B.
Euler graph
- C.
Hamiltonian circuit
- D.
Hamiltonian graph
Correct Answer
A. Euler circuitExplanation
An Euler circuit is the best graph for this scenario because it is a path that visits every edge exactly once and ends at the same vertex where it started. In this case, the city wants to start at the garage, go down each street only once, and end at the garage, which aligns with the properties of an Euler circuit.Rate this question:
-
- 7.
Elizabeth is planning a trip. She wants to fly out of Charlotte, visit New York, visit Hollywood, and end up at her parent's home in Dallas. Which graph would be best for this scenario?
- A.
Hamiltonian path
- B.
Hamiltonian circuit
- C.
Euler path
- D.
Euler circuit
Correct Answer
A. Hamiltonian pathExplanation
A Hamiltonian path is a path in a graph that visits every vertex exactly once. In this scenario, Elizabeth wants to visit each location (Charlotte, New York, Hollywood, and Dallas) exactly once, without revisiting any of them. Therefore, a Hamiltonian path would be the best graph for this scenario.Rate this question:
-
- 8.
Bob has to check the stop signs at every intersection in his hometown. He parks his car in the parking lot of the transportation department and needs to end up back at his car. He only wants to check each intersection one time. Which graph would be best for this scenario?
- A.
Hamiltonian circuit
- B.
Hamiltonian path
- C.
Euler path
- D.
Euler circuit
Correct Answer
A. Hamiltonian circuitExplanation
A Hamiltonian circuit is the best graph for this scenario because it allows Bob to visit each intersection exactly once and end up back at his car. In a Hamiltonian circuit, every vertex is visited exactly once, and the last vertex is connected to the first vertex, forming a closed loop. This ensures that Bob can check all the stop signs at each intersection without missing any and without having to backtrack or visit any intersection multiple times.Rate this question:
-
- 9.
Refer to the above graph and choose the best answer:
- A.
Euler path and Euler circuit
- B.
Euler path only
- C.
Euler circuit only
- D.
Neither an Euler path nor Euler circuit
Correct Answer
A. Euler path and Euler circuitExplanation
Based on the given graph, an Euler path is a path that visits every edge exactly once, while an Euler circuit is a path that starts and ends at the same vertex, visiting every edge exactly once. Since the graph in the question has a path that visits every edge exactly once and also starts and ends at the same vertex, it satisfies the conditions for both an Euler path and an Euler circuit. Therefore, the correct answer is "Euler path and Euler circuit".Rate this question:
-
- 10.
Refer to the above graph and choose the best answer:
- A.
Euler path and Euler circuit
- B.
Euler path only
- C.
Euler circuit only
- D.
Neither an Euler path nor an Euler circuit
Correct Answer
B. Euler path onlyExplanation
Based on the given graph, an Euler path is possible because it is a connected graph with exactly two vertices having an odd degree (A and C). An Euler path visits each edge exactly once and ends at a different vertex than where it started. However, an Euler circuit is not possible because there are more than two vertices with an odd degree. Therefore, the correct answer is "Euler path only".Rate this question:
-
- 11.
Use the graph above. The degree of vertex A is:
Correct Answer
1 - 12.
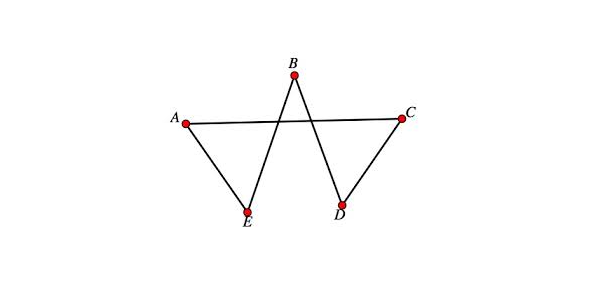
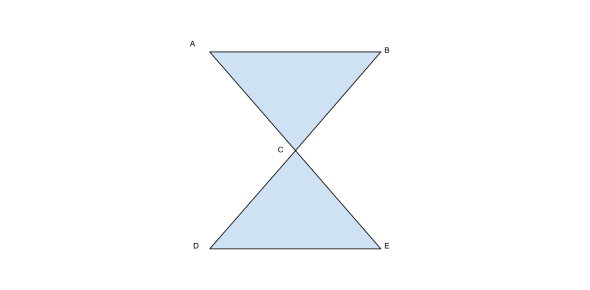
Refer to the above graph and choose the best answer:
- A.
Hamiltonian path and Hamiltonian circuit
- B.
Hamiltonian path
- C.
Hamiltonian circuit
- D.
Neither a Hamiltonian path nor Hamiltonian circuit
Correct Answer
A. Hamiltonian path and Hamiltonian circuitExplanation
Hamiltonian path: A path that visits every vertex of a graph exactly once.
Hamiltonian circuit: A Hamiltonian path that starts and ends at the same vertex.
In the given graph, the following is a Hamiltonian path:
A -> B -> D -> C -> E -> A
This path visits every vertex exactly once. It is also a Hamiltonian circuit because it starts and ends at the same vertex (A). Therefore, the graph has both a Hamiltonian path and a Hamiltonian circuit.Rate this question:
-
- 13.
Use the above graph. The degree of Vertex B is:
Correct Answer
3Explanation
The degree of a vertex in a graph is the number of edges that are connected to it. In the given graph, Vertex B is connected to three edges, namely BC, BD, and BF. Therefore, the degree of Vertex B is 3.Rate this question:
.webp "Refer to the above graph and choose the best answer:")
.webp "Refer to the above graph and choose the best answer:")
Quiz Review Timeline +
Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.
-
Current Version
-
Nov 19, 2024Quiz Edited by
ProProfs Editorial Team
Expert Reviewed by
Matt Balanda -
Mar 12, 2015Quiz Created by
Kristi Johnsen
- Algebra Quizzes
- Arithmetic Quizzes
- Calculus Quizzes
- Data Handling Quizzes
- Discrete Mathematics Quizzes
- Function Quizzes
- Measurement Quizzes
- Multiplication Quizzes
- Number Quizzes
- Percentage Quizzes
- Place Value Quizzes
- Probability Quizzes
- Problem Solving Quizzes
- Ratio Quizzes
- Shape Quizzes
- Statistics Quizzes
- Trigonometry Quizzes
Back to top