Grade 8 Math Quiz
-
To solve the following expression, which operation must you perform first? 8 + 12 (7 – 5) ÷ 6
-
+
-
- (parentheses)
-
X
-
÷
-
The Grade 8 Math Quiz is an engaging assessment designed to test and reinforce the mathematical skills and concepts typically covered in eighth-grade mathematics curricula. Math is one of the most interesting yet toughest subjects, isn't it? How about a special grade 8 math quiz right now to check your mathematics skills? If you study in 8th grade, and you See morethink your math knowledge is great, then you would not find this quiz very hard. However, the questions are not going be that easy, and they will definitely hone your skills.
This quiz serves as an essential tool for both educators and students, offering a comprehensive evaluation. With a focus on real-world applications, this quiz helps students develop problem-solving skills while strengthening their mathematical foundation. Whether you're an eighth-grade student preparing for an upcoming test or a teacher seeking to assess your students' proficiency, the Grade 8 Math Quiz provides an effective, convenient, and user-friendly platform for evaluating mathematical knowledge and promoting growth. So, what are you waiting for? Let's go!
Quiz Preview
- 2.
One way to find all the factors of 72 is to find its prime factorization. What is the prime factorization of 72?
-
3 x 3 x 3 x 2 x 2
-
6 x 3 x 2 x 2
-
2 x 2 x 2 x 3 x 3
-
9 x 2 x 2 x 3
Correct Answer
A. 2 x 2 x 2 x 3 x 3Explanation
The prime factorization of a number expresses it as the product of its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself.
To find the prime factorization of 72, we can start by dividing it by the smallest prime number, 2:
72 ÷ 2 = 36
36 ÷ 2 = 18
18 ÷ 2 = 9
9 is not divisible by 2, so we move to the next prime number, 3:
9 ÷ 3 = 3
3 ÷ 3 = 1
Therefore, the prime factorization of 72 is 2 x 2 x 2 x 3 x 3, which can also be written as 2³ x 3².Rate this question:
-
- 3.
A measuring cup has lines marking the fractions of a cup. In what order should the lines on the cup be labeled, starting with the bottom line of the measuring cup?
Correct Answer
A.Explanation
The lines on the measuring cup should be labeled in increasing order, starting with the bottom line. This is because the bottom line represents the smallest fraction of a cup, and as you move up the cup, the lines represent larger fractions. Labeling the lines in increasing order ensures that the measurements are accurate and consistent.Rate this question:
-
- 4.
Frank and Joey ordered a large pizza. Frank ate 30% of the pizza, and Joey ate 2/5 of the pizza. What percentage of the pizza did they eat in all?
-
50%
-
60%
-
70%
-
75%
Correct Answer
A. 70% -
- 5.
A student earned a grade of 80% on a math test that had 20 problems. How many problems on this test did the student answer correctly?
-
17
-
15
-
14
-
16
Correct Answer
A. 16Explanation
Since the student earned a grade of 80% on the math test, it means that they answered 80% of the problems correctly. To find out how many problems that is, we can calculate 80% of 20 (the total number of problems on the test). 80% of 20 is 16, so the student answered 16 problems correctly.Rate this question:
-
- 6.
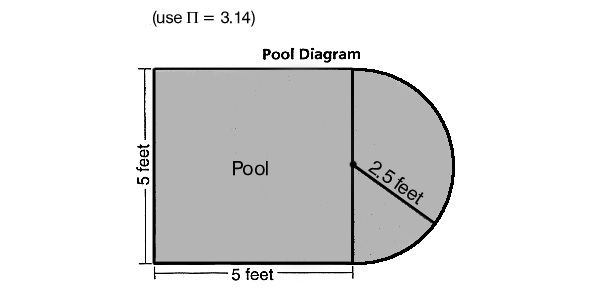
A hotel is building a children’s wading pool in the shape of a square with a semicircle on one side. A diagram of the pool is shown below. What is the perimeter of the children’s pool?
-
17.85 feet
-
27.85 feet
-
40.70 feet
-
45.70 feet
Correct Answer
A. 27.85 feetExplanation
The pool consists of a square with a semicircle on one side. The perimeter of the square is 20 feet, but we need to subtract one side (5 feet) and add the semicircle's arc length, which is 7.85 feet. This gives us 22.85 feet. To find the pool's outer perimeter, we subtract the semicircle's diameter (5 feet), resulting in 17.85 feet. Rounding to the nearest tenth gives us 17.9 feet.Rate this question:
-
- 7.
Which of the following statements about linear equations is NOT true?
-
A linear equation can be represented by a straight line on a graph.
-
The solution to a linear equation is the point where the line intersects the y-axis.
-
A linear equation has a degree of 1.
-
A linear equation can have one, infinitely many, or no solutions.
Correct Answer
A. The solution to a linear equation is the point where the line intersects the y-axis.Explanation
The solution to a linear equation is any point (or set of points) that satisfies the equation, and these points can lie anywhere along the line, not just at the y-intercept. The y-intercept is simply the point where the line crosses the y-axis, which may or may not be a solution to the equation.Rate this question:
-
- 8.
A student answered 76 problems on a test correctly and received a grade of 80%. How many problems were on the test if all the problems were worth the same number of points?
-
60
-
90
-
95
-
105
Correct Answer
A. 95 -
- 9.
A woman put $580 into a savings account for three years. The rate of interest on the account was 6½%. How much was the interest in dollars and cents? (Use simple interest)
-
$113.10
-
$337
-
$33.70
-
$104.4
Correct Answer
A. $113.10Explanation
The correct answer is $113.10. To calculate the interest for the year, we need to use the formula for simple interest: Interest = Principal x Rate x Time. In this case, the principal is $580, the rate is 6.5% (or 0.065 as a decimal), and the time is 1 year. Plugging these values into the formula, we get: Interest = $580 x 0.065 x 1 = $37.70. However, since we are asked for the interest in dollars and cents, we round this to the nearest cent, which gives us $37.70. Therefore, the interest for the year is $113.10.Rate this question:
-
- 10.
A popular game at a carnival involves a spinner. There are five sections in total. The areas of sections 1, 2, 3, and 4 are equal. The area of section 5 is twice the area of any one of the other sections. What is the probability that a player’s spin will be a 3?
Correct Answer
A.Explanation
To find the probability of landing on section 3 when spinning the carnival wheel, we need to consider the relative areas of the sections.
Let's denote the area of each section as follows:
Area of sections 1, 2, 3, and 4: A
Area of section 5: 2A (since it's twice the area of any one of the other sections)
The total area of all sections is:
Total area = 4A (for sections 1, 2, 3, and 4) + 2A (for section 5) = 6A
Now, to find the probability of landing on section 3, we'll divide the area of section 3 by the total area:
Probability of landing on section 3 = Area of section 3 / Total area
Probability of landing on section 3 = A / (6A) = 1/6
So, the probability of landing on section 3 is 1/6.Rate this question:
-
.webp)
.webp)
.webp)
Quiz Review Timeline (Updated): Apr 21, 2025 +
Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.
-
Current Version
-
Apr 21, 2025Quiz Edited by
ProProfs Editorial Team
Expert Reviewed by
Janaisa Harris -
Mar 04, 2013Quiz Created by
Goldenkeycc
Back to top